PhD defense: Michael Tope, 2-4pm 8/16, ITE325

Ph.D. Dissertation Defense

Near Optimal Sampling to Discover and Bound the Communication Rate of a Discrete Memoryless Channel

Michael Tope

Date: August 16, 2023 at 2:00pm -- 4:00pm EDT

Location: ITE 325B conference room or Webex

Committee: Drs. Joel Morris (Chair/Advisor), Tulay Adali (Co-Chair), E. F. Charles LaBerge, Christopher Marron, Anindya Roy

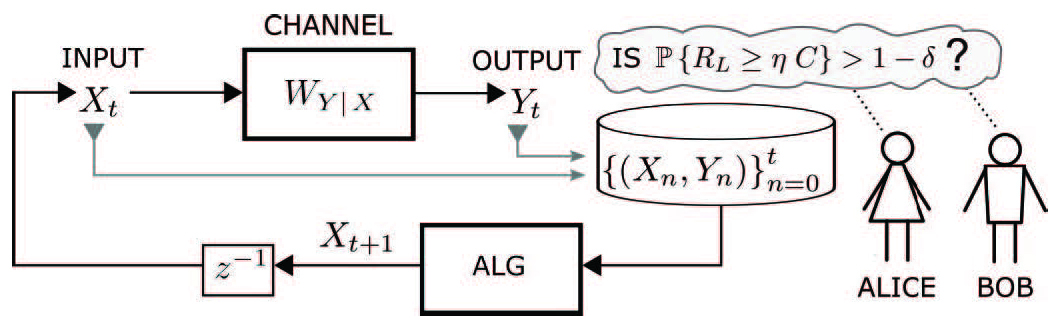
The aim of this research is to introduce, develop and evaluate active learning algorithms that provide near-optimal high-probability bounds on the channel capacity across a discrete memoryless channel (DMC), where the only information about the channel internals (i.e., the channel law) is from a set of observed input-output sample pairs (i.e., channel probes).   Channel capacity is the maximum rate (on average for each value sent into the channel) at which information can flow across the channel with an arbitrarily low error rate.

Extending results on the discrete memoryless compound channel, which is comprised of deterministic constraints on the channel law uncertainty, we first develop an offline algorithm to process an observed set of N input-output sample pairs (probes) to compute lower and upper bounds on channel capacity (such that the bounds hold with high probability).  A key ingredient of this result is our new probability approximately correct (PAC) sublevel set bound that improves the convergence rate of Sanov's Theorem from O(log(N)/N) to O(log(log(N)/N) (where the convergence rate is the 'big Oh' Bachmann-Landau limiting behavior).  The experimental (simulation) results match the analytical results.

Adapting techniques from pure-exploration multi-arm bandit problems, we further develop an online algorithm aimed at minimizing the sample complexity (i.e., the number of channel probes or samples of the DMC) required to establish a lower-bound channel rate RL that satisfies several stopping criteria, where the lower bound rate RL approaches the channel capacity with high probability.  We show that if the sample complexity of any optimal online algorithm (including a non-feasible clairvoyant algorithm that is given side information to simplify the analysis) is O(N) samples, then our online algorithm requires less than O(N*log(log(N))) sequential channel probes. Thus, we prove that our algorithm is within a sub-logarithmic factor of optimal (i.e. near optimal).

The results of this research may provide a deeper general understanding of active machine learning algorithms.